Teollisesti valmistettavia kubitteja04.01.2021
Viime vuosina yleiseurooppalainen yhteistyö yhdessä ranskalaisen CEA-Letin kanssa on tutkinut jokapäiväisien transistoreiden käyttöä kubitteina. Leti valmistaa piikiekolle transistorimaisia piirejä, joista Kööpenhaminan yliopiston Niels Bohr -instituutin tutkijat ovat havainneet, että nämä teollisesti valmistetut piirit soveltuvat sellaisten kubittien alustaksi, joka kykenee siirtymään toiseen ulottuvuuteen, mikä on merkittävä askel toimivalle kvanttitietokoneelle. Yksi piirien pääominaisuuksista on kvanttipisteiden kaksiulotteinen ryhmitys. Tai tarkemmin kaksi kertaa kaksi hilaa kvanttipisteitä. "Olemme osoittaneet, että voimme toteuttaa yksittäisen elektronin ohjauksen jokaisessa näistä kvanttipisteistä. Tämä on erittäin tärkeää kubitin kehityksen kannalta, koska yksi mahdollisista tapauksista tuottaa kubitteja on käyttää yksittäisen elektronin spiniä. Joten tämän tavoitteen saavuttaminen hallitsemalla yksittäisiä elektroneja ja tehdä se kvanttipisteiden 2D-ryhmässä oli meille erittäin tärkeää", sanoo postdoc-tutkija Fabio Ansaloni. Elektronin spinin käyttö on osoittautunut edulliseksi kubittien toteuttamisessa. Itse asiassa niiden "hiljainen" luonne tekee spineistä heikosti vuorovaikutteisia kohisevan ympäristön kanssa, mikä on tärkeä vaatimus suorituskykyisten kubittien tuottamiseksi. Kvanttitietokoneiden prosessorien laajentaminen toiseen ulottuvuuteen on osoittautunut välttämättömäksi kvanttivirheiden korjausrutiinien tehokkaammalle toteuttamiselle. Kvanttivirhekorjaus antaa mahdollisuuden tuleville kvanttitietokoneille olla vikasietoinen yksittäisiä kubittivirheitä vastaan laskelmien aikana. Apulaisprofessori Anasua Chatterjee lisää: "Työmme alkuperäisenä ajatuksena oli tehdä ryhmä spinkubitteja ja päästä aina yksittäisiin elektroneihin ja pystyä hallitsemaan ja siirtelemään niitä. Yksittäisien elektronien kaksiulotteiset ryhmät ovat sitten todella iso tavoite, koska se alkaa näyttää siltä, mitä ehdottomasti tarvitaan kvanttitietokoneen rakentamiseen. Edistyminen on kolminkertaista, tutkijat selittävät: Ensinnäkin piirirakenteiden valmistaminen teollisesti skaalautuvasti on välttämätöntä, jotta voi tehdä isompia ryhmiä esimerkiksi pienille kvanttisimulaattoreille. Toiseksi, kvanttitietokoneen tekemiseksi tarvitaan matriisi kahdessa ulottuvuudessa ja tapa liittää ulkomaailma kuhunkin kubittiin. Jos kullakin kubitilla on yhteys toisiinsa syntyy epärealistinen määrä yhteyksiä. Nyt onnistuttiin osoittamaan, että voi olla yksi portti elektronia kohden ja samalla portilla voi sekä lukea että hallita. Ja lopuksi näiden työkalujen avulla tutkijat pystyivät siirtämään ja vaihtamaan yksittäisiä elektroneja hallitusti ryhmän ympärillä, mikä on itsessään haaste." Kaksiulotteiset taulukkomatriisit voivat hallita virheitä. Huipputeknisillä fyysisillä kubiteilla ei vielä ole alhaista virhesuhdetta, mutta jos niitä on riittävästi yhdistetty 2D-ryhmään, ne voivat pitää toisensa kurissa. Tämä on vielä lisäetu nyt toteutetusta 2D-ryhmästä. Niels Bohr -instituutissa saatu tulos osoittaa, että nyt on mahdollista hallita yksittäisiä elektroneja ja suorittaa koe ilman magneettikenttää. Joten seuraava vaihe on etsiä spinin ilmiöitä magneettikentän avulla. Tämä on välttämätöntä yhden ja kahden kubitin -porttien toteuttamiseksi ryhmän yksittäisten kubittien välillä. Teoria on osoittanut, että kourallinen yhden ja kahden kubitin portteja, joita kutsutaan täydellisiksi kvanttiporttien sarjoiksi, ovat riittäviä mahdollistamaan universaalin kvanttilaskennan. Aiheesta aiemmin: Elektronin geometria määritelty Laveampaa kvantti-informaation vaihtoa |
| 24.04.2024 | Akku ja superkonkka yhteen soppii |
| 23.04.2024 | Kaareva datalinkki esteitä ohittamaan |
| 22.04.2024 | Kvanttimateriaali lupaa uutta puhtia aurinkokennoille |
| 21.04.2024 | Läpimurto lupaa turvallista kvanttilaskentaa kotona |
| 20.04.2024 | Yksi atomikerros kultaa ja molekyylikorjaaja |
| 19.04.2024 | Uusia ja yllättäviä topologiota |
| 18.04.2024 | Kvanttivalo syntyy renkaassa ja lähtee kiertueelle |
| 17.04.2024 | Fononit ja magnonit kaveraavat |
| 16.04.2024 | E-nenälle ihmisen tasoinen hajuaisti |
| 15.04.2024 | Valo valtaa alaa magnetismissa |
|
Siirry arkistoon » |

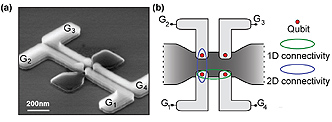 (a) Kuvassa kvanttipisterakenne, jonka neljä kvanttipistettä voidaan muodostaa piihin (tummanharmaa) neljällä itsenäisellä ohjausportilla (vaaleanharmaa). (b) Kaaviokuva kaksiulotteisesta matriisirakenteesta. Kukin kubitti voi olla vuorovaikutuksessa lähimmän naapurinsa kanssa kaksiulotteisessa ryhmässä.
(a) Kuvassa kvanttipisterakenne, jonka neljä kvanttipistettä voidaan muodostaa piihin (tummanharmaa) neljällä itsenäisellä ohjausportilla (vaaleanharmaa). (b) Kaaviokuva kaksiulotteisesta matriisirakenteesta. Kukin kubitti voi olla vuorovaikutuksessa lähimmän naapurinsa kanssa kaksiulotteisessa ryhmässä.