Kiertymiä ja laaksoja17.09.2021
Toistensa suhteen kiertyneet grafeenirakenteet löydettiin muutama vuosi sitten. Niissä elektronit ovat vahvassa vuorovaikutuksessa toistensa kanssa ja sen seurauksena materiaali voi esimerkiksi muuttua suprajohtavaksi. ETH:n ja Texas Austin yliopiston yhteinen tutkijaryhmä on nyt havainnut uuden tilan kahden kaksikerroksisen grafeenin kiertyneessä rakenteessa. Tässä tilassa negatiivisesti varautuneet elektronit ja positiivisesti varautuneet aukot korreloivat keskenään niin voimakkaasti, että materiaali ei enää johda sähkövirtaa. "Perinteisissä kokeissa, joissa grafeenikerrokset ovat kiertyneet noin yhden asteen verran toisiinsa nähden, elektronien liikkuvuuteen vaikuttaa kerrosten välinen kvanttimekaaninen tunnelointi", kertoo tutkija Peter Rickhaus. "Uudessa kokeessamme sitä vastoin kierrämme kahta kaksikerroksista grafeenia yli kaksi astetta toisiinsa nähden, joten elektronit eivät voi enää tunneloitua kaksoiskerrosten väliin." Tämän seurauksena sähkökentän avulla voidaan luoda elektroneja toiseen kaksoiskerrokseen ja aukkoja toiseen. Odotusarvo oli, että kaksi grafeenin kaksoiskerrosta muodostaa vielä paremman johteen. Mutta jos sähkökenttää säädetään niin, että tuplakerroksissa on sama määrä elektroneja ja aukkoja niin vastus kasvaa yhtäkkiä jyrkästi. Yllättävä ilmiö selittyi sillä, että kyseessä on uudenlainen tiheysaalto. Yleensä niitä syntyy yksiulotteisissa johteissa, kun elektronit johtavat yhdessä sähkövirtaa ja myös järjestäytyvät avaruudellisesti aalloiksi. Siten ETH-tutkijoiden kokeessa elektronit ja aukot yhdistyvät nyt toisiinsa sähköstaattisen vetovoiman avulla ja muodostavat siten kollektiivisen tiheysaallon. Tämä tiheysaalto koostuu kuitenkin nyt sähköisesti neutraaleista elektroni-aukko pareista, joten kaksi kaksoiskerrosta yhdessä eivät voi enää johtaa sähkövirtaa. Kyseessä on täysin uusi korreloitujen elektronien ja aukkojen tila, jolla ei ole varausta mutta tämä neutraali tila voi kuitenkin siirtää informaatiota tai johtaa lämpöä. Elektronit ja aukot ovat tässä perustilassaan mikä tarkoittaa, että spontaaninen hajoaminen ei rajoita niiden käyttöikää.
Tutkimusraportissaan tutkijat esittävät tavan ajaa laaksotoimintoja yksikerroksisessa tai koskemattomassa grafeenissa, mikä muiden alan tutkijoiden mielestä ei ole ollut mahdollista. Atomisen ohuissa grafeenikerroksissa on elektronilaaksoja, mutta materiaalin luontaisen symmetrian vuoksi niitä pidettiin hyödyttöminä laaksotoiminnoissa. Yksi houkuttelevimmista näkökohdista laaksotoimien suorittamisessa grafeenissa on, että se on mahdollista tehdä huoneenlämmössä. Tutkijat visioivat, että heidän havaintonsa voivat tasoittaa tietä pienikokoisille kvanttitietokoneille, jotka voivat toimia huoneenlämmössä. Aiheista aiemmin: Uusia ominaisuuksia moiré-superhiloissa Taikamateriaali moneksi elektroniseksi rakenteeksi Twistroniikkaa paksummillakin materiaaleilla Magnetismin ja ferrosähkön kierteitä grafeenissa |
| 19.04.2024 | Uusia ja yllättäviä topologiota |
| 18.04.2024 | Kvanttivalo syntyy renkaassa ja lähtee kiertueelle |
| 17.04.2024 | Fononit ja magnonit kaveraavat |
| 16.04.2024 | E-nenälle ihmisen tasoinen hajuaisti |
| 15.04.2024 | Valo valtaa alaa magnetismissa |
| 13.04.2024 | Nanorakenteilla energiaa haihtuvasta vedestä |
| 12.04.2024 | Bolometrit kubitteja mittaamaan |
| 11.04.2024 | Kudottavia ohuita puolijohdekuituja |
| 10.04.2024 | 2D-antenni tehostaa hiilinanoputkien valontuottoa |
| 09.04.2024 | Lisää tiedonsiirtokapasiteettia langattomaan viestintään |
|
Siirry arkistoon » |


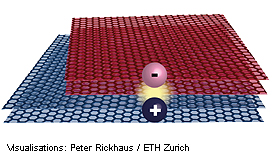 Tutkijat ovat havainneet uuden aineen tilan: toisiinsa nähden kiertyneissä grafeenikerroksissa kaksi sähköjohdetta muodostaa eristeen.
Tutkijat ovat havainneet uuden aineen tilan: toisiinsa nähden kiertyneissä grafeenikerroksissa kaksi sähköjohdetta muodostaa eristeen.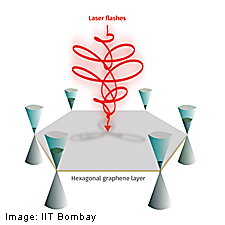 Laaksotroniikka (valleytronics) on kehittyvä ala, jossa laaksoja - paikallisia minimimääriä kiintoaineiden energiakaistarakenteessa - käytetään koodattaessa, käsiteltäessä ja tallennettaessa kvantti-informaatiota. Vaikka grafeenin uskottiin olevan epäsopiva laaksotroniikalle sen symmetrisen rakenteen vuoksi, Intian Bombayn teknologiainstituutin ja Max-Born -instituutin tutkijat ovat äskettäin osoittaneet, että näin ei ole.
Laaksotroniikka (valleytronics) on kehittyvä ala, jossa laaksoja - paikallisia minimimääriä kiintoaineiden energiakaistarakenteessa - käytetään koodattaessa, käsiteltäessä ja tallennettaessa kvantti-informaatiota. Vaikka grafeenin uskottiin olevan epäsopiva laaksotroniikalle sen symmetrisen rakenteen vuoksi, Intian Bombayn teknologiainstituutin ja Max-Born -instituutin tutkijat ovat äskettäin osoittaneet, että näin ei ole.