Topologisia ulottuvuuksia kvanttitietotekniikalle04.06.2020
Topologiset eristeet kiinnostavat alan tutkijoita koska niitä voidaan mahdollisesti käyttää suprajohteina tulevaisuuden elektroniikassa. Näiden materiaalien lisäksi on olemassa toinen luokka, joka tunnetaan korkeamman asteen topologisina eristeinä (HOTI). Näissä kolmiulotteisissa kiteissä on johtavia, yhden ulottuvuuden kanavia, jotka kulkevat vain tietyillä kidereunoilla. Tällaiset materiaalit soveltuvat puolestaan kvanttilaskennan sovelluksiin. Asiantuntijat olettavat, että puolimetallisella vismutilla on joitain toisen asteen topologisen materiaalin ominaisuuksista. Lisäksi on teoretisoitu että myös puolimetalli volframiditelluridin (WTe2) atomisesti ohuet kerrokset käyttäytyvät kuin toisen asteen topologiset eristeet – eli ne johtavat sähköä häviöttömästi reunoilla, kun taas loppuosa kerroksesta käyttäytyy kuin eriste. Baselin yliopiston fysiikan laitoksen ja Sveitsin nanotieteiden instituutin professori Christian Schönenbergerin johtama ryhmä on nyt analysoinut pieniä volframiditelluridikiteitä, jotka koostuvat yhdestä 20 kerrokseen. Analysoimalla pääkiteen sisäistä virtausta, tutkijat havaitsivat lukuisia hitaasti rappeuttavia värähtelyjä, jotka tutkijoiden mukaan viittaavat siihen, että suuri osa virrasta kulkee kapeita reunoja pitkin. Nämä havainnot tukevat teoreettisia ennusteita, että volframiditelluridi on korkeamman asteen topologinen materiaali. Tämä avaa uusia mahdollisuuksia topologiselle suprajohtavuudelle, jolla voi olla sovelluksia esimerkiksi kvanttilaskentaan”, sanoo Christian Schönenberger, joka tutkii topologista suprajohtavuutta tiettyjen kaksiulotteisten materiaalien pinoina. Kvantti Hall efekti löydettiin jo 1980-luvulla kaksiulotteisesta elektronijärjestelmästä ja laboratoriot ympäri maailmaa pyrkivät nykyään tekemään 3D-topologisia suprajohteita kvanttilaskentaa varten. Yhdysvaltalaiset (Rice, UC Berkeley) ja saksalaiset fyysikot (KIT) ovat löytäneet yllättäviä todisteita siitä, että kvantti Hall -vaikutus - on "tullut todellisuudeksi" topologisiin suprajohteisiin, joita voitaisiin käyttää vikasietoisen kvanttitietokoneen rakentamiseen. Kvantti Hall -efekti on sittemmin löydetty 2D-materiaaleista ja laboratoriot ympäri maailmaa pyrkivät tekemään kolmiulotteisia topologisia suprajohteita kvanttilaskennassa käytettäväksi. "Tässä työssä olemme osoittaneet, että tietyn 3D-topologisten suprajohteiden luokan tulisi osoittaa pinnallaan 2D-elektronisten tilojen "energiapinoja", kertoo Ricen professori Matthew Foster. "Jokainen näistä pinotuista tiloista on vankka "uudelleeninkarnaatio" yksittäisestä erityistilasta, joka esiintyy 2D-kvantti Hall -ilmiössä." "Eli hienosäädetty topologinen kvanttifaasimuutos 2D:ssä, on "uudelleeninkartoitunut" yleisemmäksi pintatilaksi suuremman ulottuvuuden massalle". "Mielenkiintoisia asioita näissä 3D-järjestelmissä tapahtuu vain rajoilla mutta nyt rajat eivät ole 1D-reunatiloja, vaan ne ovat 2D-pintoja." toteaa Foster. Vaikka tutkijat osoittivat vahvaa laskennallista näyttöä yllättävästä yhteydestä topologisen aineen 2D- ja 3D-faasien välillä nämä topologiset suprajohteet on vielä toteutettava kokeellisesti, toteavat tutkijat yliopistonsa tiedotteessa. "Meillä on nyt todisteita siitä, että kolme viidestä 3D-topologisesta vaiheesta on sidottu 2D-vaiheisiin, jotka ovat kvantti Halli -ilmiön versioita ja kaikki kolme 3D-vaihetta voitaisiin toteuttaa "topologisissa suprajohteissa", "Foster toteaa. Aiheesta aiemmin: Suprajohtavuutta ja topologiaa Kvanttisimulointia topologisista eristeistä |
| 24.04.2024 | Akku ja superkonkka yhteen soppii |
| 23.04.2024 | Kaareva datalinkki esteitä ohittamaan |
| 22.04.2024 | Kvanttimateriaali lupaa uutta puhtia aurinkokennoille |
| 21.04.2024 | Läpimurto lupaa turvallista kvanttilaskentaa kotona |
| 20.04.2024 | Yksi atomikerros kultaa ja molekyylikorjaaja |
| 19.04.2024 | Uusia ja yllättäviä topologiota |
| 18.04.2024 | Kvanttivalo syntyy renkaassa ja lähtee kiertueelle |
| 17.04.2024 | Fononit ja magnonit kaveraavat |
| 16.04.2024 | E-nenälle ihmisen tasoinen hajuaisti |
| 15.04.2024 | Valo valtaa alaa magnetismissa |
|
Siirry arkistoon » |


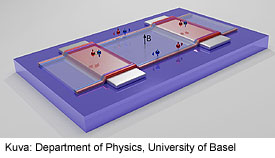 Kaavio kokeellisesta järjestelystä: Atomisesti ohut kerros volframiditelluridia sijaitsee kahden hopeakontaktin välissä. Virta kulkee materiaalin läpi vain erittäin kapeilla ulkoreunan kanavilla.
Kaavio kokeellisesta järjestelystä: Atomisesti ohut kerros volframiditelluridia sijaitsee kahden hopeakontaktin välissä. Virta kulkee materiaalin läpi vain erittäin kapeilla ulkoreunan kanavilla.